
初めまして!
ようこそ!
れんがのーとへ!
TRPGプレイヤーのレンgaです!
@rengatrpg
ラプラスの悪魔・シュレディンガーの猫・ノアの方舟・マーフィーの法則
など、『カタカナ+漢字』の言葉ってなんかいいですよね!
シナリオタイトルに使ってみたり、キャラの二つ名にしてみたり、いろいろな使い方も出来るでしょう!
今回は、そんな『カタカナ+漢字』の言葉を200語句以上集めて、その言葉の意味などが分かるようにまとめました!
数が多いので、目次から調べて探してみてください♪
※随時、どんどん更新していきます!
- シナリオタイトルで悩んでいる人
- かっこいい言葉が知りたい人
- アイデアが欲しい人
あ行
あ
アーネシの魔女
アーネシの魔女……アーネシの曲線(アーネシのきょくせん) (伊: la versiera di Agnesi, 英: witch of Agnesi) またはアーネシの魔女は直交座標における方程式
Wikipedia
{\displaystyle y={\frac {c^{3}}{x^{2}+c^{2}}}}
すなわち {\displaystyle (x^{2}+c^{2})y-c^{3}=0} によって表される曲線である。
アイオロスの球
アイオロスの球(アイオロスのたま、aeolipile)またはヘロンの蒸気機関(ヘロンのじょうききかん、Hero engine)は羽根のない簡単な半径流蒸気タービンであり、中央の水容器を熱することにより回転する。チップジェットまたはロケットのように、タービンから蒸気を噴出することにより、その反動力でトルクを生み出す。紀元1世紀ごろ、アレクサンドリアのヘロンがこの装置を文献に記し、多くの文献が彼が発明者だとしている。
Wikipedia
アインシュタインの十字架
アインシュタインの十字架(Einstein Cross)とは、銀河[Y88] Gと、[Y88] Gによってもたらされた重力レンズ効果で4個に分裂したクエーサーQSO 2237+030の組み合わせである。アインシュタインクロスとも呼ばれる[5] 。
Wikipedia
アキレウスの盾
アキレウスの盾(アキレウスのたて、アキレスの盾とも)とは、ギリシア神話の英雄アキレウスがヘクトールと戦う時に用いた盾である。
Wikipedia
アスクレピオスの杖
アスクレピオスの杖(アスクレピオスのつえ、英語: Rod of Asclepius)とは、ギリシア神話に登場する名医アスクレピオス(アスクレーピオス)の持っていた蛇(クスシヘビ)の巻きついた杖。医療・医術の象徴として世界的に広く用いられているシンボルマークである。
Wikipedia

アステカの水晶髑髏
水晶髑髏(すいしょうどくろ)とは、水晶で作られた人間の頭蓋骨模型のことである。
Wikipedia
アフロディーテの泉
アプロディーテー(古典ギリシア語
Wikipedia
:ΑΦΡΟΔΙΤΗ, Ἀφροδίτη, Aphrodītē)またはアプロディタ(アイオリス方言
:ΑΦΡΟΔΙΤΑ, Ἀφροδιτα, Aphrodita)は、愛と美と性を司るギリシア神話の女神で、オリュンポス十二神の一柱である。美において誇り高く、パリスによる三美神の審判で、最高の美神として選ばれている。また、戦の女神としての側面も持つ。日本語では、アプロディテ、アフロディテ、アフロディーテ、アフロダイティ(英: Aphrodite)などとも表記される。
アポロニウスの円
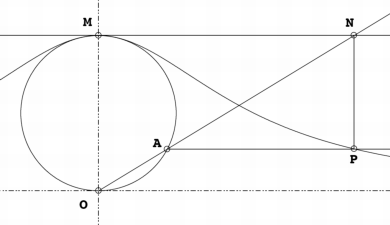
アポロニウスの円(アポロニウスのえん)は、2定点A・Bをとり、点PをAP:BPが一定となるように(但しAP≠BP)したときの点Pの軌跡である。ペルガのアポロニウスの名前を残す。
Wikipedia

アマルテイアの城砦
アマルテイア(古希: Ἀμάλθεια, Amaltheia, ラテン語: Amalthea)は、ギリシア神話に登場するゼウスの育ての親である。ラテン語ではアマルテアという。彼女は時に山羊として表現され、クレータ島のイーデー山の洞窟で幼いゼウスに乳を与えたとされる。また時にニュムペーとされ、ゼウスに山羊の乳を与えて育てたとされる。
Wikipedia
アリアドネの糸
アリアドネー(古希: Ἀριάδνη, Ariadnē)は、クレータ王ミーノースと妃パーシパエーのあいだの娘である。テーセウスがクレータ島の迷宮より脱出する手助けをしたことで知られる。アリアドネーという名は「とりわけて潔らかに聖い娘」を意味するので、この名からすると本来女神であったと考えられる。
Wikipedia
日本語では長母音を省略してアリアドネとも表記される。
アリストテレスの提灯
アリソフの気候区分
アリソフの気候区分(アリソフのきこうくぶん)とはソビエト連邦の気候学者であるB・P・アリソフ(Алисов, Борис Павлович、B. P. Alissow〔B. P. Alissovとも表記、1891年 – 1972年〕)が考案した気候区分である。緯度と地表の状態を大気循環によって区分したものである。
Wikipedia

アルキメデスの螺旋
代数螺旋(だいすうらせん)は代数的な式によって表される螺旋である。アルキメデスの螺旋、放物螺旋、双曲螺旋、リチュースなどがある。対数螺旋は代数螺旋には含まれない。
Wikipedia
アルゴーの船
アルゴー船(アルゴーせん、Argo)は、ギリシア神話に登場する巨大な船の名前である。アルゴ船、アルゴー号とも。
Wikipedia
船大工でプリクソスの子アルゴス(英語版)が建造したので、彼の名から命名された。イオールコスの英雄イアーソーンがコルキスの黄金の羊の毛皮(金羊毛すなわちゴールデン・フリース)を求める冒険のために建造された。アルゴー船の乗組員には、勇士50人が募集され、これに応じてヘーラクレース、双子のカストールとポリュデウケース、オルペウス、リュンケウスなど、ギリシア神話で活躍する英雄たちが乗り込んだとされる。彼らをアルゴナウタイと称する。

アレクサンドリアの大灯台
アレクサンドリアの大灯台(アレクサンドリアのだいとうだい、Lighthouse of Alexandria)は、紀元前3世紀頃にエジプトのアレクサンドリア湾岸のファロス島に建造された灯台。ファロス島の大灯台、あるいはアレクサンドリアのファロスとも呼ばれる。
Wikipedia
ファロス島は、アドリア海に同名の島(現在のフヴァル島)があるが、それとは別で、アレクサンドリア港の一方の端に人工の埋め立てにより出来上がった半島の突端にあった小さな島である。世界の七不思議のひとつ。ただし、ビザンチウムのフィロンの選出した七不思議には含まれていない。14世紀の二度の地震によって全壊したが、七不思議の中ではギザの大ピラミッドに次ぐ長命な建造物だった。

アロンの杖
アロンの杖(アロンのつえ、英語: Aaron’s rod)は、『旧約聖書』の『出エジプト記』に登場するモーセがイスラエルの神から授かり、モーセと兄アロンが使っていたとされる不思議な杖。
Wikipedia
アンスコムの例
アンスコムの例(Anscombe’s quartet)あるいはアンスコムの数値例とは、回帰分析において、散布図はそれぞれ異なるのに回帰直線やその他の統計量が同じになってしまう現象について、統計学者のフランク・アンスコム(英語版)が1973年に紹介した例である。回帰分析をする前に散布図を確認し傾向を把握することの重要性、そして外れ値が統計量に与える影響の大きさを示している。
Wikipedia
い
イージスの盾
イージスの盾とは、ギリシア神話に登場する防具。主神ゼウスのものとも、ゼウスが娘の女神アテーナーに与えたものともされる。
Wikipedia
イズンの林檎
黄金の林檎(おうごんのりんご)は、さまざまな国や民族に伝承される民話や説話の果実である。
Wikipedia
よく見られるのは、醜怪な敵役が隠したり盗んだりした黄金の林檎を、ヘーラクレースやファト・フルモス(英語版)といった英雄が取り戻すという主題である。あるいは北欧神話のように、黄金の林檎は神の食べ物、また不死の源として描かれている。
印欧語で”Apple”は果実全般を指す語である。「黄金の林檎」という語も、必ずしも現代で言う林檎を指すわけではなく、後述するように「黄金の林檎」と同一視されるのは他の果実であることが多い。
インドラの矢
インドラ(Indra、梵: इंद्र、इन्द्र)はバラモン教、ヒンドゥー教の神の名称である。省略しない名称は「サンスクリット語:śakro devānām indraḥ[注釈 1]、パーリ語:Sakko devānaṃ indo」で「強力な神々の中の帝王」を意味する。「シャクラ(śakra)」や「サッカ(sakka)」とも呼ばれる。
Wikipedia
う
ウィグナーの友人
ウィリアムズの接続器
ウィルソンの湾曲
ウォードの箱
ウォードの箱(ウォードのはこ、英語名:Wardian case)は、ナサニエル・バグショー・ウォード(1791年-1868年)が1829年頃にイギリスの首都ロンドンで発明したガラス器。発明はウォードの偶然の発見によるものであった。ウォードの箱は主に植物の運搬に使用され、近代における先駆的な植物栽培用の容器となった。
Wikipedia

ウロボロスの輪
ウロボロス (ouroboros, uroboros) は、古代の象徴の1つで、己の尾を噛んで環となったヘビもしくは竜を図案化したもの。
Wikipedia

え
エヴェレットの多世界解釈
エヴェレットの多世界解釈(エヴェレットのたせかいかいしゃく、英: many-worlds interpretation; MWI)とは、量子力学の観測問題における解釈の一つである。 プリンストン大学の大学院生であったヒュー・エヴェレット3世が1957年に提唱した定式を元に、ブライス・デウィット(英語版)によって提唱された。
Wikipedia
エイムズの部屋
エイムズの部屋は、錯視を起こす歪んだ部屋。ヘルマン・フォン・ヘルムホルツの著作の影響もあるが、 1946年にアメリカの科学者アデルバート・エイムズ・ジュニア(英語版)により発明され、翌年に作られた。
Wikipedia
お
オッカムの剃刀
オッカムの剃刀(オッカムのかみそり、英: Occam’s razor、Ockham’s razor)とは、「ある事柄を説明するためには、必要以上に多くを仮定するべきでない」とする指針。もともとスコラ哲学にあり、14世紀の哲学者・神学者のオッカムが多用したことで有名になった。様々なバリエーションがあるが、20世紀にはその妥当性を巡って科学界で議論が生じた。「剃刀」という言葉は、説明に不要な存在を切り落とすことを比喩しており、そのためオッカムの剃刀は思考節約の原理や思考節約の法則、思考経済の法則とも呼ばれる。またケチの原理と呼ばれることもある。
Wikipedia
オルレアンの噂
オルレアンの噂 ……忽然と客の消えるブティック(こつぜんときゃくのきえるブティック)は、都市伝説の一つ。とあるブティックの試着室に入った女性が、いつまで待っても出てこない。一緒に来た夫や恋人、友人が店員に尋ねても、「そんな客は来なかった」と返されてしまい、結局行方不明になってしまう、というもの。
Wikipedia
行方不明者のその後には、様々なバリエーションがある。
か行
か
カーラーの救命曲線
カーラーの救命曲線 (カーラーのきゅうめいきょくせん Golden Hour Principle) とは、心臓停止、呼吸停止、大量出血の経過時間と死亡率の目安をグラフ化したもので、応急手当の講習などで良く使われるグラフである。
Wikipedia
カニッツァの三角形
カニッツァの三角形(カニッツァのさんかくけい、Kanizsa triangle)は錯視図形の一つで、イタリアの心理学者ガエタノ・カニッツァにより1955年に発表された。周辺の図形とともに、白い正三角形が知覚されるが、実際には中心の三角形は物理的に存在しない。この効果は、主観的輪郭(subjective contour)と呼ばれる。また、この白い三角形は、周辺よりも明るく見えるが、実際には中心と周辺の輝度は等しい。パックマン刺激とも言う。
Wikipedia

ガフの部屋
ガフの部屋(ガフのへや)とは、ヘブライ人の伝説にある、神の館にある魂の住む部屋のこと。
Wikipedia
ガブリエルの喇叭
ガブリエルのホルン(英: Gabriel’s Horn)またはガブリエルのトランペットは、有限の体積と無限の表面積を併せもつ幾何学的な空間図形である。その名称は、有限が無限(神)と結びつくこの現象を、最後の審判を告げる笛を吹くという伝承の大天使ガブリエルへなぞらえたものである。この図形の性質を調べた最初の人は、17世紀イタリアの物理学者兼数学者のエヴァンジェリスタ・トリチェリで、トリチェリのトランペット(英: Torricelli’s trumpet)とも呼ばれる。
Wikipedia
カントールの塵
カノッサの屈辱
カノッサの屈辱(カノッサのくつじょく、ドイツ語: Gang nach Canossa、イタリア語: Umiliazione di Canossa)は、聖職叙任権をめぐってローマ教皇グレゴリウス7世と対立していたローマ王ハインリヒ4世が、1077年1月25日から3日間に及んで雪が降る中、カノッサ城門にて裸足のまま断食と祈りを続け、教皇による破門の解除を願い、教皇から赦しを願ったことを指す。
Wikipedia
き
ギザの大金字塔
ギザの大ピラミッド(ギザのだいピラミッド、英語: Great Pyramid of Giza)は、エジプトのギザに建設された、世界の七不思議で唯一現存する建造物である。紀元前5世紀のギリシャの歴史家ヘロドトスの『歴史』において、「クフ王のピラミッド」として報告されているが、この時点で建設から2000年以上経過していた。
Wikipedia
「ケオプス(クフ)王は50年間統治したと言われている。ケオプス王が崩御した後、兄弟のケフラン(カフラー)が王となった。ケフランもピラミッドを造った。それはケオプスのピラミッドよりも12メートルほど低かった。だがそれ以外は同じような大きさのピラミッドだった。ケフラン王は56年間国を統治した。その後はケオプス王の息子ミケリノス(メンカウラー)が王位を継承した。ミケリノス王は父親よりも小さなピラミッドを残した。」
建築年代については諸説あり、一般的にエジプト第4王朝のファラオ、クフ王の墳墓として紀元前2560年頃に20年前後かけて建築されたと考えられている。
完成時の高さ146.6mは、14世紀にリンカン大聖堂が完成するまで世界で最も高い建造物であった。

キチンの波
キチンの波(キチン循環)は、約40ヶ月の周期を持つ景気循環です。 企業の在庫投資が起因すると考えられています。 ほかに、在庫循環(在庫投資循環)、小循環、短期波動などの呼び方があります。 景気循環は、周期の長さにより、キチンの波、ジュグラーの波、クズネッツの波、コンドラチェフの波の4つにわけられます。
金融大学
ギャルの角笛
ギャラルホルン(古ノルド語: Gjallarhorn、Giallarhorn、ギャッラルホルン、ギャルの角笛)は、北欧神話においてアースガルズの門番であるヘイムダルが持つ角笛で、ラグナロクの到来を告げるという。
Wikipedia
ギュゲースの指輪
ギュゲースの指輪(ギュゲースのゆびわ)は、自在に姿を隠すことができるようになるという伝説上の指輪である。リュディアの人ギュゲスが手に入れ、その力で王になったという。
Wikipedia
く
クルルカンの降臨
クズネッツの波
クズネッツの波(クズネッツ循環)は、約20年の周期を持つ景気循環です。 建築物の需要が起因すると考えられています。 ほかに、建築循環という呼び方があります。 景気循環は、周期の長さにより、キチンの波、ジュグラーの波、クズネッツの波、コンドラチェフの波の4つにわけられます。
金融大学
クラインの壺
クラインの壺(クラインのつぼ、英語: Klein bottle)は、境界も表裏の区別も持たない(2次元)曲面の一種で、主に位相幾何学で扱われる。
Wikipedia
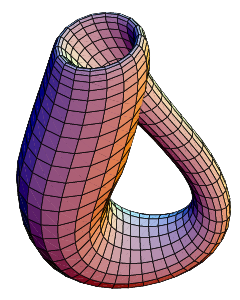
クルスキーの手形
け
ゲーデルの不完全性定理
ゲーデルの不完全性定理(ゲーデルのふかんぜんせいていり、英: Gödel’s incompleteness theorems、独: Gödelscher Unvollständigkeitssatz)又は単に不完全性定理とは、数学基礎論における重要な定理で、クルト・ゲーデルが1930年に証明したものである。不完全性定理が示したものは、数学用語での「特定の形式体系{\displaystyle P}において決定不能な命題の存在」であり、一般的な意味での「不完全性」とは無関係である。すなわち不完全性定理以降の時代にも、数学上の意味で「完全」な理論は存在し続けているが、“不完全性定理は数学や理論の「不完全性」を証明した”というような誤解が一般社会・哲学・宗教・神学等によって広まり、誤用されている。
Wikipedia
ケーニヒスベルクの橋
一筆書き(ひとふでがき)とは、広い意味では「筆記具を平面から一度も離さず線図形を描く」ことである。狭い意味では、これに加えて「同じ線を二度なぞらない(点で交差するのはかまわない)」という条件が加わる。筆記体のdは、前者の意味では一筆書きであるが、後者の意味では一筆書きではない。
Wikipedia
以下は後者の狭い意味での一筆書きについて記す。
三角形「△」や四角形「□」は一筆書き可能だが、十字「+」は一筆書きできない。また、五芒星や白星「☆」、六芒星「✡」は一筆書き可能だが、アスタリスク「*」は一筆書きができない。このように、一筆書きできる図形とできない図形がある。
「与えられた図形が一筆書き可能かどうか」という問題の例として、「ケーニヒスベルクの橋の問題」(独: Königsberger Brückenproblem)が知られている。なお、ケーニヒスベルクとは実際にあった場所の名前である。
ケーララの赤い雨
ケーララの赤い雨(ケーララのあかいあめ)は、2001年7月25日から9月23日にかけて、インド南部のケーララ州に降った赤い色の雨。ひどい時には服がピンクに染まるほどだった。色は黄、緑、黒に近い場合もあった。なお、ケーララ州で色が付いた雨が降ったという報告は1896年にもなされており、それ以来、数回報告されている。
Wikipedia
当初は、雨に流星由来の放射性物質が含まれているためと考えられた。しかし、インド政府から依頼された調査チームは、地元に生える藻類の胞子由来と結論した。
2006年の初めまで、ケーララの赤い雨が話題になることは少なかった。しかし、2006年始めにマハトマ・ガンジー大学(英語版)のゴドフリー・ルイ(英語版)とサントシ・クマルが「この細胞は地球外から来たものだ」とする仮説を発表したことから、マスコミが注目するようになった。

ゲッセマネの園
ゲッセマネ(Gethsemane、希: Γεθσημανι、ヘブライ語: גת שמנים Gat-Šmânim、アラム語: גת שמנא Gaṯ-Šmānê)はエルサレムのオリーブ山の北西麓にあった地名で、新約聖書の福音書で知られる。ゲツセマネとも表記し、オリーブの木の植えられた庭園風の場所だったためゲッセマネの園(その)とも呼ばれている。
Wikipedia
ケッペンの気候区分
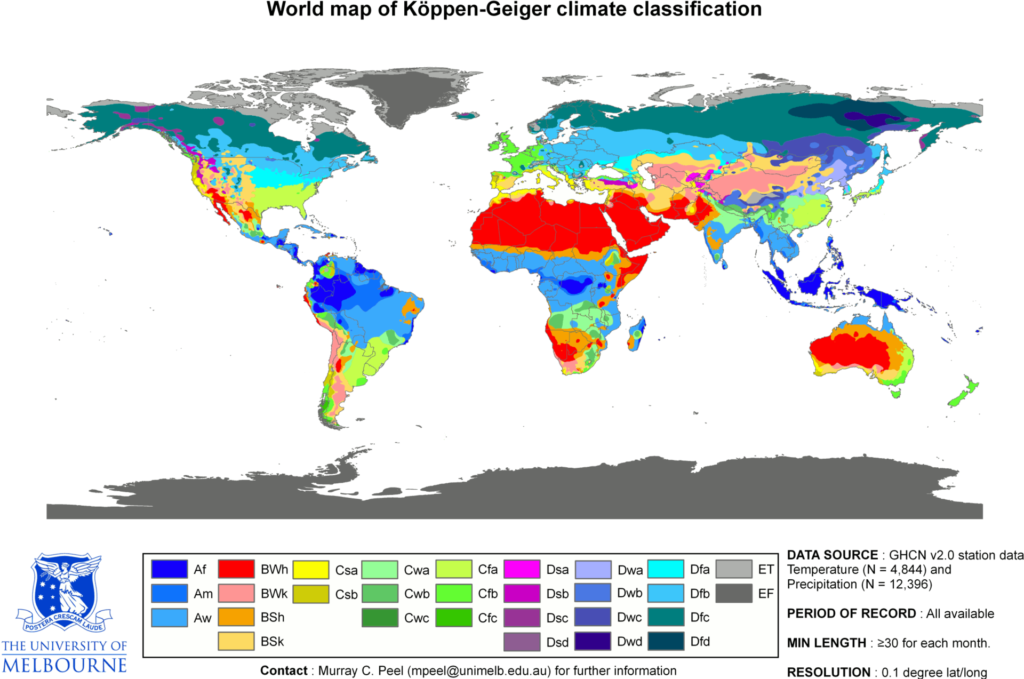
ケッペンの気候区分(ケッペンのきこうくぶん、ドイツ語: Köppen-Geiger Klassifikation)は、ドイツの気候学者ウラジミール・ペーター・ケッペンが、植生分布に注目して考案した気候区分である。
Wikipedia
ケントの花
ケントの花(ケントのはな、英:Flower of Kent)は、セイヨウリンゴの品種名である。1665年にアイザック・ニュートンが万有引力を発見したのは、この品種のリンゴが落果するのを見たのがその契機であると伝わり、「ニュートンのリンゴ」、「ニュートンのリンゴの木」などの別名でも知られる 。
Wikipedia
こ
コスタリカの石球
コスタリカの石球(コスタリカのせっきゅう、Stone spheres of Costa Rica)とは、1930年代の初め、コスタリカの密林で発見された石の球体である。現在までに200個以上が発見されている。石球を含む考古遺跡4箇所は「ディキスの石球のある先コロンブス期首長制集落群」の名で世界遺産リストに登録されている。
Wikipedia

コソの遺物
コソの点火プラグ(コソのてんかプラグ)とは、1961年2月13日にアメリカのカリフォルニア州オランチャ(Olancha)から北東に10 kmほど離れた、コソ山脈(Coso Range)で発見された点火プラグのことである。コソ加工物と呼称される場合が多い。
Wikipedia
通常、この点火プラグがオーパーツとして紹介される際には、プラグを覆っていた石化した土を地質学者が鑑定を行ったところ、50万年前という鑑定結果が出されたと言われることが多い。
コモンズの悲劇
コモンズの悲劇(コモンズのひげき、英: Tragedy of the Commons)とは、多数者が利用できる共有資源が乱獲されることによって資源の枯渇を招いてしまうという経済学における法則。共有地の悲劇ともいう。
Wikipedia
コリオリの力
コリオリの力(コリオリのちから、仏: force de Coriolis)とは、回転座標系上で移動した際に移動方向と垂直な方向に移動速度に比例した大きさで受ける慣性力(見かけ上の力)の一種であり、コリオリ力、転向力(てんこうりょく)ともいう。1835年にフランスの科学者ガスパール=ギュスターヴ・コリオリが導いた。
Wikipedia
回転座標系における慣性力には、他に、角速度変化に伴うオイラー力と回転の中心から外に向かって働く遠心力がある。
ゴルゴダの丘
ゴルゴタの丘(ゴルゴタのおか、ヘブライ語: גבעת הגולגולתא、ギリシア語: Κρανίου Τόπος、ラテン語: Calvariae Locus)は、エルサレムの丘。
Wikipedia
ゴルディアスの結び目
ゴルディアスの結び目(ゴルディアスのむすびめ、英: Gordian Knot)は、古代アナトリアにあったフリギアの都ゴルディオンの神話と、アレクサンドロス大王にまつわる伝説である。この故事によって、手に負えないような難問を誰も思いつかなかった大胆な方法で解決しまうことのメタファー「難題を一刀両断に解くが如く」(英: To Cut The Gordian Knot )として使われる。ゴルディオンの結び目、ゴルディオスの結び目とも。
Wikipedia
コルニュの螺旋
クロソイド曲線(クロソイドきょくせん、(英: clothoid curve)とは緩和曲線の一種である。 「クロソイド」という名は、人間の運命の糸を紡ぐとされるギリシア神話の女神クローソーに由来するもので、イタリアの数学者アーネスト・チェザロによって名付けられた。光学分野においては、同曲線はオイラー螺旋やコルニュ螺旋とも呼ばれる。
Wikipedia
コロンブスの卵
コンドラチェスの波
さ行
さ
サマイパタの砦
サラディンの鷹
サラディンの鷹……金色の鷹は「サラディンの鷹」とも呼ばれ、12世紀にサラディンによって使用され、20世紀の汎アラブ主義のシンボルとされた。エジプトは1984年に「クライシュ族の鷲」から現在の「サラディンの鷹」に変更した。
Wikipedia

し
シーシュポスの岩
シーシュポス(古希: Σίσυφος, Sīsyphos, ラテン語: Sisyphus)は、ギリシア神話に登場する人物である。長母音表記を略してシシュポス、シジフォス、シシュフォスとも省略される。コリントスの創建者。徒労を意味する「シーシュポスの岩」で知られる。
Wikipedia
ジェヴォーダンの獣
ジェヴォーダンの獣(ジェヴォーダンのけもの、仏: La bête du Gévaudan)は、18世紀のフランス・ジェヴォーダン地方(現在はロゼール県の一部)に出現した、オオカミに似た生物。1764年から1767年にかけマルジュリド山地周辺に現れ、60人から100人の人間を襲った。獣が何であったかは、現在も議論されている。 事件は未確認動物学と陰謀の両方の面の憶測がされている。
Wikipedia
15世紀に首都パリに迫ったオオカミの群れの史実が有名であるが、18世紀後半のフランスでは、ソワソンやペリゴール(現在のドルドーニュ県)など各地でオオカミ被害が相次いでいた。

ジェリコの壁
エリコの壁(エリコのかべ)は、ヘブライ聖書に書かれているエリコ(イェリコ)の街の城壁である。ウォールズ・オブ・ジェリコ (Walls of Jericho) とも呼ばれる。
Wikipedia
ジェリコの喇叭
ジャバウォックの詩
『ジャバウォックの詩』(ジャバウォックのし、Jabberwocky )は、ルイス・キャロルの児童文学『鏡の国のアリス』で記述されたナンセンス詩である。『ジャバウォックの詩』は、英語で書かれた最も秀逸なナンセンス詩であると考えられている。
Wikipedia
この詩では、ジャバウォックと呼ばれる正体不明の怪物が名前のない主人公によって打ち倒されるという出来事が、叙事詩のパロディによる形式で描写される。文中に出てくる単語の多くは、キャロルによって創作されたかばん語である。
ジュグラーの波
景気循環(けいきじゅんかん、英: Business cycle)とは、経済全体の活動水準である景気において、循環的に見られる変動のことである。景気変動(けいきへんどう)、景気の波(けいきのなみ)とも呼ばれる。景気が一定の原因により決まった周期で恒常的・法則的に循環すると考える説を景気循環論という。
Wikipedia
シュレディンガーの猫
シュレーディンガーの猫(シュレーディンガーのねこ、シュレディンガーとも、英: Schrödinger’s cat)は、1935年にオーストリアの物理学者エルヴィン・シュレーディンガーが発表した量子力学のパラドックスを指摘するための思考実験。ボーアら量子論主流派のコペンハーゲン解釈を身近なものに当てはめることによって、その問題を指摘しようとした。
Wikipedia
本来は量子力学を批判するために用いられたものであったが、むしろ量子の世界の特異さを説明する例示として逆用され、後にエヴェレットの多世界解釈が生まれるきっかけの1つにもなった。量子論におけるいくつかの解釈や理論をシュレーディンガーの猫を使って説明するという例もよくある。

ジョンバールの分岐点
ジョンバール分岐点(ジョンバールぶんきてん、英: Jonbar hinge 、英: Jonbar pointとも)は、SFの用語である。
Wikipedia
特にタイムトラベルに関する物語において、歴史上の重要な一点で時間軸が分岐し、世界が枝分かれして元の世界と平行した別の世界が生まれているという解釈を基に、パラレルワールドが生まれる瞬間を指す。
この用語は、ジャック・ウィリアムスンのSF小説「航時軍団」(The Legion of Time、1938年)に由来する。 主人公ジョン・バール(John Barr)の1つの行動、小さな決断(彼がある瞬間に磁石と小石のどちらを拾い上げるか)が分岐点となり、ユートピア社会「ジョンバール」(Jonbar)と独裁主義が支配する「ギロンチ」(Gyronchi)の二つの平行世界が生まれることになる。
す
スースロフの漏斗
スカンデルベグの鷹
双頭の鷲(そうとうのわし、ギリシア語: Δικέφαλος αετός、ドイツ語: Doppeladler、英語: Double-headed eagle)とは、鷲の紋章の一種で、頭を2つ持つ鷲の紋章。
Wikipedia
主に東ローマ帝国や神聖ローマ帝国と、関連したヨーロッパの国家や貴族などに使用された。現在でもセルビア、アルバニア、ドイツ、ロシアなどの国章や、ギリシャ正教会などで使用されている。
スキャモンの発育曲線
スクーンの石
ストックホルムの血浴
ストックホルムの血浴(スウェーデン語: Stockholms blodbad)とは、デンマーク王クリスチャン2世が1520年にスウェーデンのストックホルムで行なったスウェーデン人に対する処刑ないし粛清である
Wikipedia

スペルガの悲劇
スペルガの悲劇(スペルガのひげき、伊:Tragedia di Superga)とは、1949年5月4日、イタリア・トリノ郊外の丘陵地、通称「スペルガの丘」で起きた航空機墜落事故のこと。乗員・乗客31名全員が犠牲となり、死亡者の中にはイタリアのプロサッカークラブ、ACトリノの選手18名と監督以下スタッフ5名が含まれていた。
Wikipedia
スレイマンの星
モロッコの国旗(モロッコのこっき、Flag of Morocco)は深紅の色で預言者ムハンマドを象徴しており、緑の五芒星「スレイマン(ソロモン)の印章」が表されている。
Wikipedia
現王朝のアラウィー朝が始まった17世紀ころには赤旗が用いられていたが、1912年に「ほかの多くの赤旗と区別するため」緑の星が付け加えられた。
憲法第7条で「王国のしるしは、中央に5つの稜を持つ緑の星を伴った赤い旗である」と定められている。

せ
セフィロトの樹
生命の樹(せいめいのき、英語: Tree of Life)は、旧約聖書の創世記(2章9節以降)にエデンの園の中央に植えられた木。命の木とも訳される。生命の樹の実を食べると、神に等しき永遠の命を得るとされる。
Wikipedia
カバラではセフィロトの木(英語: Sephirothic tree)という。
ヤハウェ・エロヒム(エールの複数形、日本語では主なる神と訳されている)がアダムとエヴァをエデンの園から追放した理由は、知恵の樹の実を食べた人間が、生命の樹の実までも食べて永遠の生命を得、唯一絶対の神である自身の地位が脅かされる(ユダヤ伝承では知恵の樹の実と生命の樹の実をともに食べると、神に等しき存在になるとされているので)事を恐れたためである。

セントアントニウスの舌
セントエルモの火
セントエルモの火(セントエルモのひ、英: St. Elmo’s fire)は、悪天候時などに船のマストの先端が発光する現象。
Wikipedia
激しいときは指先や毛髪の先端が発光する。航空機の窓や機体表面にも発生することがある。
セントテレサの手
そ
ソディの六球連鎖
ソディの6球連鎖(ソディのろくきゅうれんさ、英: Soddy’s hexlet)とは、イギリスの化学者フレデリック・ソディが1936年に学術雑誌ネイチャーに発表した、幾何学の定理に現れるネックレス状の球の連鎖である。
Wikipedia

ソロモンの指輪
ソロモンの指輪(ソロモンのゆびわ)は、偽典のひとつとされる『ソロモンの遺訓(英語版)』(『ソロモンの聖約』)に記された、ヤハウェの命を受けた大天使ミカエルよりソロモン王に授けられた指輪である。
Wikipedia
ソロモンの指輪は真鍮と鉄でできており、様々な悪霊を使役する権威を与えると伝えられている。
た行
た
タタールの軛
タタールのくびき(タタールの軛)またはモンゴル=タタールの軛(モンゴル=タタールのくびき、ロシア語: Монголо-татарское иго、英語: Tataro-Mongol Yoke)とは、13世紀前半に始まったモンゴルのルーシ侵攻とそれにつづくモンゴル人(モンゴル=タタール)によるルーシ(現在のロシア・ウクライナ・ベラルーシ)支配を、ロシア側から表現した用語である。現在のロシア人などの祖先であるルーシ人のモンゴル=タタールへの臣従を意味するロシア史上の概念である。
Wikipedia
ダーウィンの海
ダモクレスの剣
ダモクレスの剣(ダモクレスのつるぎ、- のけん。英語:sword of Damocles, Sword of Damocles)とは、栄華の最中にも危険が迫っていることや、そのような危険、または、常に身に迫る一触即発の危険な状態をいう。
Wikipedia
ダビデの星
ダビデの星(ダビデのほし)は、ユダヤ教、あるいはユダヤ民族を象徴するしるし。二つの正三角形を逆に重ねた六芒星(ヘキサグラム)といわれる形をしておりイスラエルの国旗にも描かれている。
Wikipedia

ち
チェーホフの銃
チェーホフの銃(チェーホフのじゅう、英語: Chekhov’s gun)とは、小説や劇作におけるテクニック・ルールの1つ。
Wikipedia
つ
ツァラトゥストラの翼
『ツァラトゥストラの翼』(ツァラトゥストラのつばさ、英: The Zarathustra’s Wings)は、岡嶋二人による日本のゲームブック。1986年2月に講談社スーパーシミュレーションノベルスとして刊行され、1990年5月に文庫化された。
て
ディオファントスの一生
ティンダロスの猟犬
ティンダロスの猟犬(ティンダロスのりょうけん、The Hounds of Tindalos)は、クトゥルフ神話作品に登場する架空の生物。
Wikipedia
初出は『ウィアード・テイルズ』誌1929年3月号に掲載されたフランク・ベルナップ・ロングの小説「ティンダロスの猟犬(The Hounds of Tindalos)」。
時間が生まれる以前の超太古、異常な角度をもつ空間に住む不浄な存在とされる。
絶えず飢え、そして非常に執念深い。四つ足で、獲物の「におい」を知覚すると、その獲物を捕らえるまで、時間や次元を超えて永久に追い続ける。獲物を追う様子から「猟犬」と呼ばれるが、犬とは全く異なる存在である。

テオドシウスの城壁
テセウスの船
テセウスの船(テセウスのふね、英: Ship of Theseus)はパラドックスの1つであり、テセウスのパラドックスとも呼ばれる。ある物体(オブジェクト)の全ての構成要素(部品)が置き換えられたとき、基本的に同じであると言える(同一性=アイデンティティ)のか、という問題である。
Wikipedia
デデキントの切断
デデキント切断(デデキントせつだん、英: Dedekind cut)、あるいは単に切断 (独: Schnitt) とは、リヒャルト・デデキントが考案した数学的な手続きで、実数論の基礎付けに用いられる。
Wikipedia
テニスコートの誓い
球戯場の誓い(きゅうぎじょうのちかい、仏: Serment du Jeu de paume、英: Tennis Court Oath)とは、フランス革命直前の1789年6月20日、三部会の第三身分議員がヴェルサイユ宮殿の球戯場(ジュ・ド・ポームのコート)に集まり、憲法制定まで解散しないことを誓い合った事件。英語の重訳からテニスコートの誓いとも呼ばれる。
Wikipedia
テレネの木
テネレの木(Arbre du Ténéré)は、ニジェール中央部のテネレ砂漠に1本だけ立っていた木。地球上で最も孤立した場所に立っていた木として知られ、最も近い他の木から200km以上も離れた場所に立っていた。
Wikipedia
デュラックの海
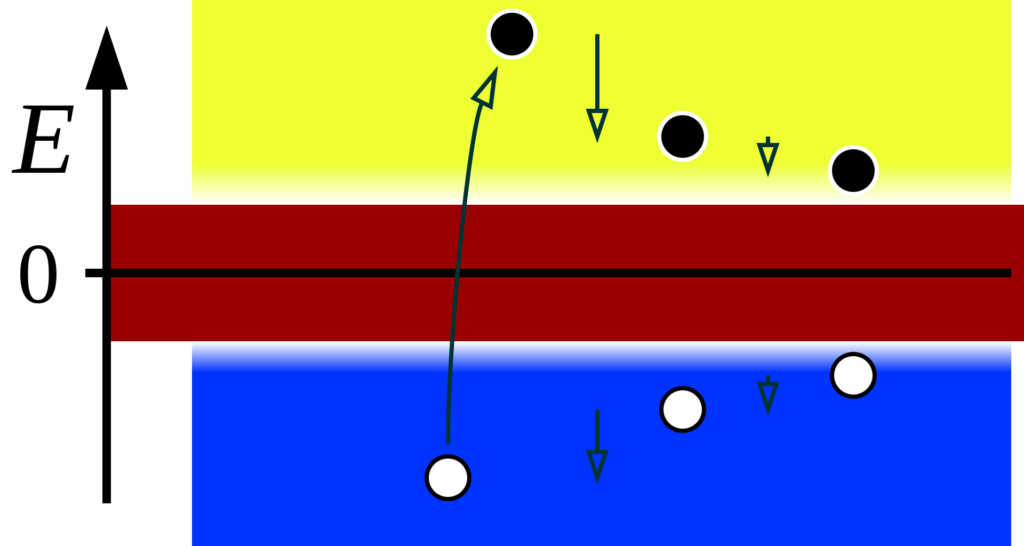
ディラックの海(ディラックのうみ、英: Dirac sea)とは、真空状態が負のエネルギーを持つ電子によって完全に占められている状態であるというモデル。
Wikipedia
ディラック方程式の解が負のエネルギー状態を持つことによって生じる問題を回避すべく、英国の物理学者ポール・ディラックが空孔理論の中で提唱した。ディラックは、電子が満たす相対論的な量子力学の基礎方程式として、ディラック方程式を導いたが、この方程式は負のエネルギーの解を持つ。
デリーの鉄柱
デリーの鉄柱(デリーのてっちゅう)とは、インド・デリー市郊外のクトゥブ・ミナール内にある錆びない鉄柱のこと。チャンドラヴァルマンの柱とも。1993年に「デリーのクトゥブ・ミナールとその建造物群」として世界遺産に登録された。
Wikipedia

デルポイの神託
デルポイ(古代ギリシア語: Δελφοι / Delphoi)は、古代ギリシアのポーキス地方にあった都市国家(ポリス)。パルナッソス山のふもとにあるこの地は、古代ギリシア世界においては世界のへそ(中心)と信じられており、ポイボス・アポローンを祀る神殿で下される「デルポイの神託」で知られていた。古代デルポイの遺跡はユネスコの世界遺産(文化遺産)に登録されている。
Wikipedia
日本語では「デルフォイ」「デルファイ」と表記されることも多い。英語表記(Delphi)、フランス語表記(Delphes)や現代ギリシア語発音に基づく「デルフィ」も用いられる。遺跡の西にはデルフィの名をもつ集落があり、また遺跡を含む自治体の名前にもなっている。
テルミドールの反動
テルミドールのクーデターとは、1794年7月27日(フランス革命暦II年テルミドール9日)に起きた、フランス革命時におけるジャコバン派独裁に対立する勢力によるクーデターである。これによりマクシミリアン・ロベスピエールとその同志であるルイ・アントワーヌ・ド・サン=ジュスト、ジョルジュ・クートン、フィリップ=フランソワ=ジョゼフ・ル・バ(en)らが失脚し、ある者は処刑され、ある者は自殺した。 テルミドール9日の反動、テルミドール反動とも呼ばれる。
Wikipedia
デンデラの電球
デンデラの電球はエジプト、デンデラのハトホル神殿にある石造りのレリーフとして彫られたモチーフ。これは現代的な電気照明装置に見た目が似ている。境界科学による仮説はデンデラの電球が古代エジプト人が持つ高度な電気技術を描いていると示唆している。しかし、主流のエジプト学者はエジプト神話からの象徴的なイメージの典型的なものを表しているとみなしている。これはそれぞれ安定と多産の象徴であるジェド柱と中にヘビを孕むハスの花を描いている。
Wikipedia
と
トゥキディデスの罠
トゥキディデスの罠(英: The Thucydides Trap)は、古代アテナイの歴史家、トゥキディデスにちなむ言葉で、戦争が不可避な状態まで従来の覇権国家と、新興の国家がぶつかり合う現象を指す。アメリカ合衆国の政治学者グレアム・アリソンが作った造語。
Wikipedia
ドベネックの桶
ドリンカーの救命曲線
トレヴィの泉
トレヴィの泉(トレヴィのいずみ、イタリア語: Fontana di Trevi)は、ローマにある最も巨大なバロック時代の人工の泉(噴水)である。ローマでも有数の観光名所として賑わっている。トレビの泉、トレドの泉とも呼称される。
Wikipedia
トレスカの断面
トロイの木馬
トロイアの木馬(トロイアのもくば)は、ギリシア神話のトロイア戦争において、トロイア(イーリオス)を陥落させる決め手となったとされる装置である。トロイの木馬とも言われる。木でできており、中に人が隠れることができるようになっていた。 転じて、内通者や巧妙に相手を陥れる罠を指して「トロイの木馬」と呼ぶことがある。
Wikipedia

ドロレスの叫び
ドロレスの叫び(スペイン語: Grito de Dolores)は、1810年9月16日に当時スペイン領だったメキシコで、最初の独立指導者ミゲル・イダルゴ・イ・コスティージャ(Miguel Hidalgo y Costilla)によって発せられた演説であり、これをきっかけにしてメキシコ独立革命が始まった。
Wikipedia
な行
な
ナスカの地上絵
ナスカの地上絵(ナスカのちじょうえ)は、ペルーのナスカ川とインヘニオ川に囲まれた乾燥した盆地状の高原の地表面に「描かれた」幾何学図形、動植物の絵。
Wikipedia

に
ニュートンの林檎
ニュートンの林檎……ケントの花(ケントのはな、英:Flower of Kent)は、セイヨウリンゴの品種名である。1665年にアイザック・ニュートンが万有引力を発見したのは、この品種のリンゴが落果するのを見たのがその契機であると伝わり、「ニュートンのリンゴ」、「ニュートンのリンゴの木」などの別名でも知られる 。
Wikipedia
ぬ
ヌルハチの墓
ヌルハチの墓……福陵(ふくりょう、満州語:ᡥᡡᡨᡠᠷᡞᠩᡤᠠ
Wikipedia
ᠮᡠᠩᡤᠠᠨ、転写:hūturingga munggan)は、中国遼寧省の瀋陽市渾南区天柱山にある、清の前身・後金の初代皇帝であるヌルハチ、及びホンタイジの生母であるイェヘナラ氏(孝慈高皇后)の陵墓。
ね
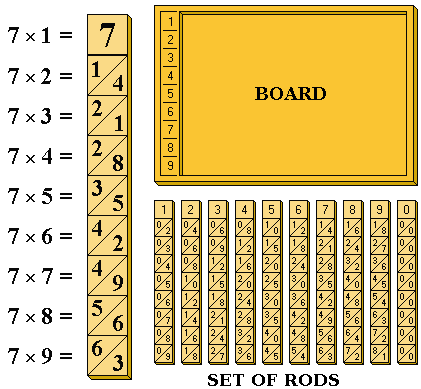
ネイピアの骨
ネイピアの骨 (ネイピアのほね、Napier’s bones) は、ジョン・ネイピアが発明したかけ算や割り算などを簡単に行うための道具である。
Wikipedia
ネブカドネザルの鍵
ネプチューンの噴水
ネメアーの獅子
ネメアーの獅子(ネメアーのしし、古希: Νεμέος λέων, Neméos léōn)はギリシア神話に登場するライオン。ネメアの谷に住み着き、人や家畜を襲ったとされる。
Wikipedia
母はエキドナ、父はその子オルトロスとも、テューポーンともいわれる。エピメニデースによるとネメアーの獅子を生んだのはセレーネーであり、恐ろしい身震いをしたときに地上に降ってきたという。またヒュギーヌスによるとセレーネーはネメアーの獅子を2つの入り口がある洞窟で育てた。

の
ノアの方舟
ノアの方舟(ノアのはこぶね、英語: Noah’s Ark)は、旧約聖書の『創世記』(6章-9章)に登場する、大洪水にまつわる、ノアの方舟物語の事。または、その物語中の主人公ノアとその家族、多種の動物を乗せた方舟自体を指す。「はこぶね」は「方舟」のほか、「箱舟」「箱船」などとも記される。
Wikipedia

ノックスの十戒
ノックスの十戒(ノックスのじっかい、Knox’s Ten Commandments)はロナルド・ノックスが1928年に“The Best of Detective Stories of the Year 1928”(邦題『探偵小説十戒』)で発表した、推理小説を書く際のルールである。本記事では単に「十戒」と表記する。
Wikipedia
S・S・ヴァン=ダインによる「ヴァン・ダインの二十則」と並んで推理小説の基本指針となっている。日本では江戸川乱歩が『幻影城』の中で紹介している。
なお、「十戒」を意図的に破った作品や、「十戒」の記述を逆手にとったトリックを用いた作品も数多く存在している。ノックス自身も「十戒」を破った作品を発表しており(ヴァン=ダインも同様)、また十戒の前置きで「どうして自分でこんなことを考えたか分からない」旨を述べているなど、ユーモア精神から冗談半分に書かれたとする見方も多い。
は行
は
ハーベイロードの前提
ハーヴェイロードの前提(英語:Harvey Road presumption)とは、ケインズ経済学において、「政府は民間経済主体に比べて経済政策の立案能力・実行能力に優れている」という仮説。増税と政府の裁量権拡大を正当化するケインズ経済学を批判する意味で使われることが多い。経済学者ロイ・ハロッドが、『ケインズ伝』で、ジョン・メイナード・ケインズが生まれ育ったケンブリッジのハーヴェイ・ロード6番地にちなんで、ケインズの政治思想につけた言葉である。
Wikipedia
バールベックの巨石
バールベックの巨石は、中東・西アジアのレバノンにある宗教都市バールベックで、世界遺産として登録されているジュピター神殿の土台として使われている3つの巨石のこと。
Wikipedia

ハイディンガーの刷子
ハイディンガーのブラシ (Haidinger’s brush) は内視現象のひとつで、偏光している可視光を見たときにヒトの視野の中心部にかすかに現れる束状の模様をいう。
Wikipedia
ハイリゲンシュタットの遺書
ハイリゲンシュタットの遺書(独: Heiligenstädter Testament)は、ルートヴィヒ・ヴァン・ベートーヴェンが1802年10月6日にハイリゲンシュタット(今日ではウィーンの一部)において、甥であるカール(ドイツ語版)と弟のヨハンに宛てて書いた手紙である。ベートーヴェンが亡くなった後の1827年3月にこの文書はアントン・シンドラーとシュテファン・フォン・ブロイニンクによって発見され、10月に公表された。
Wikipedia
ハイルブロンの怪人
ハイルブロンの怪人(ハイルブロンのかいじん、ドイツ語: Heilbronner Phantom,英語: Phantom of Heilbronn)とは1993年から2008年にかけて、ドイツをはじめヨーロッパ各地で起きた、殺害事件を含む40件の犯罪現場でのDNA採取で検出された同一のDNAから推定された、架空の犯人。
Wikipedia
バグダッドの電池
バグダッド電池(バグダッドでんち)とは、現在のイラク、バグダッドで製造されたとされる土器の壺である。
Wikipedia
電池であるという意見と、そうではないとする意見が存在する。
ハノイの塔
ハノイの塔(ハノイのとう、Tower of Hanoi)はパズルの一種。 バラモンの塔または ルーカスタワー(Lucas’ Tower)とも呼ばれる。
Wikipedia

バビロンの空中庭園
バビロンの空中庭園(バビロンのくうちゅうていえん、Hanging Gardens of Babylon)は、古代ギリシアの数学者・フィロンが選んだ「世界の七不思議」の建造物の一つの屋上庭園。バビロンの吊り庭園(バビロンのつりていえん)ともいう。
Wikipedia
名前からは、重力に逆らって空中に浮かぶ庭園が連想されるが、実際には高台に造られた庭園である。

パブロフの犬
条件反射(じょうけんはんしゃ)とは、動物において、訓練や経験によって後天的に獲得される反射行動のこと。ソビエト連邦の生理学者イワン・パブロフによって発見され、パブロフの犬の実験で有名になった。
Wikipedia
「パブロフの犬」のような唾液分泌の条件付けは、長い間、哺乳類などの高等生物にのみ起こると考えられていたが、条件付けのモデル生物としての意味ではアメフラシなどにも起こる。また、2006年には東北大学の研究によりゴキブリにも起こることがわかった。2014年には扁形動物であるプラナリアでも条件反射が獲得できることが判明した。
バベルの塔
バベルの塔(バベルのとう、ヘブライ語: מגדל בבל)は、旧約聖書の「創世記」中に登場する巨大な塔。
Wikipedia
神話とする説が支配的だが、一部の研究者は紀元前6世紀のバビロンのマルドゥク神殿に築かれたエ・テメン・アン・キのジッグラト(聖塔)の遺跡と関連づけた説を提唱する。
実現不可能な天に届く塔を建設しようとして、崩れてしまったといわれることにちなんで、空想的で実現不可能な計画を比喩的に「バベルの塔」という。

バンディアガラの断崖
バンディアガラの断崖(バンディアガラのだんがい、仏: La falaise de Bandiagara)は、マリ共和国のドゴン族居住地域となっている断崖。その壮観な自然環境と、マルセル・グリオールの紹介によって広く知られるようになったドゴン族の文化が保持されている地域であることから、ユネスコの世界遺産に登録されている。
Wikipedia
この断崖の標高差は500mであり、幅は150kmに及んでいる。この断崖の所々や、断崖の裾野に、ドゴン族はおよそ700の村落を作り、25万人ほどが暮らしている。ドゴン族がこの地に定住を始める以前にはテラン族 (Tellem) たちの居住地として使われていたが、ドゴン族の流入によって追い出された。
パンドラの箱
パンドーラー(古希: Πανδώρα, Pandōrā)は、ギリシア神話に登場する女性で、神々によって作られ人類の災いとして地上に送り込まれた。人類最初の女性とされる。パン(Παν)は「全てのもの」であり、パンドーラーは「全ての贈り物」を意味する。
Wikipedia
ハンロンの剃刀
ハンロンの剃刀(ハンロンのかみそり、英: Hanlon’s razor)とは、次の文で表現される考え方のことである。
Wikipedia
ひ
ピサの斜塔
ピサの斜塔(ピサのしゃとう、イタリア語: Torre di Pisa)は、イタリアのピサ市にあるピサ大聖堂の鐘楼であり、世界遺産「ピサのドゥオモ広場」を構成する観光スポットである。高さは地上55.86m、階段は296段あり、重量は14,453t、地盤にかかる平均応力は50.7tf/m2と見積もられている。一時傾斜の増大と倒壊の危惧があったがその後の処置により、当分問題ないと判断されている(後述)。5.5度傾いていたが、1990年から2001年の間に行われた工事によって、現在は約3.99度に是正されている。また、定刻ごとに鳴る鐘の音は、備え付けられている鐘を実際に鳴らすと傾斜に影響を及ぼす恐れがあるために、スピーカーから流されてい。かつてのガリレオの実験に対して行われた異端審問の弾圧に関連してローマ法王が詫びの公式声明を塔の頂上にて行ったことも有名。
Wikipedia

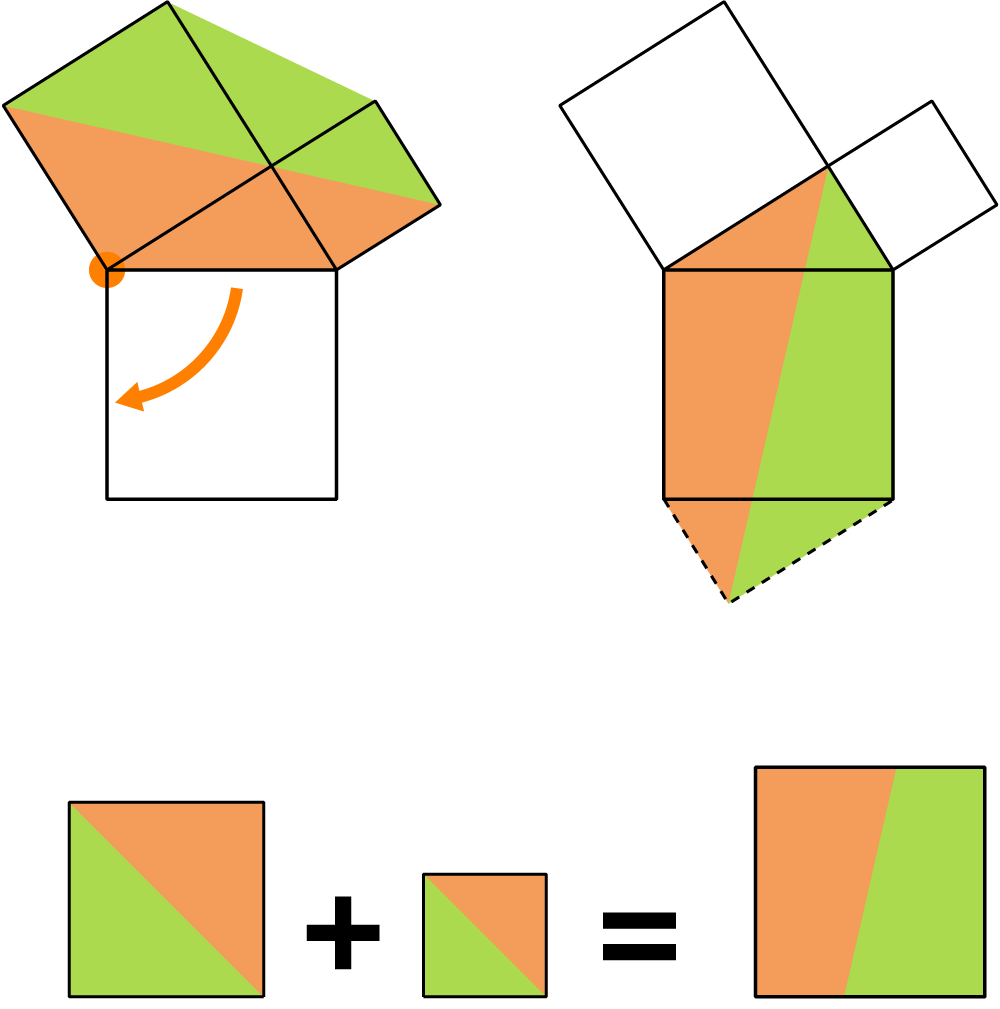
ピタゴラスの定理
ピタゴラスの定理(ピタゴラスのていり、英: Pythagorean theorem)は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は
Wikipedia
{\displaystyle c^{2}=a^{2}+b^{2}}
が成り立つという等式の形で述べられる。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。
ヒトラーの電動鋸
グロスフスMG42機関銃(グロスフスMG42きかんじゅう、Maschinengewehr 42(マシーネンゲヴェーア ツヴァイウントフィアツィヒ)、MG42またはMG-42)は、第二次世界大戦時の1942年にナチス・ドイツにより開発・製造された汎用機関銃である。
Wikipedia

ヒュギエイアの杯
ヒュギエイアの杯(ヒュギエイアのさかずき、英: Bowl of Hygieia)とは、ギリシア神話に登場する名医アスクレピオスの娘のヒュギエイアが持っていた杯。ヘビの巻きついた杯として表現される。アスクレピオスの杖と並び医療・医術の象徴として世界的に広く用いられているシンボルマークである。特にアスクレピオスの杖が医学のシンボルとされるのに対し、ヒュギエイアの杯は薬学のシンボルとして用いられる場合が多い。
Wikipedia
ビュフォンの針
ビュフォンの針(ビュフォンのはり、英: Buffon’s needle problem)は18世紀の博物学者ジョルジュ=ルイ・ルクレール、コント・ド・ビュフォンが提起した数学上の問題である。
Wikipedia
もし床に多数の平行線を引き、そこに針を落すならば、どれかの線と針が交差する確率はどのようになるかという問題である。
積分と幾何学を使ってこの問題は解け、またこの方法を使って、モンテカルロ法で円周率の近似値を求められる。
ピュロスの勝利
ピュロスの勝利(ピュロスのしょうり、英語: Pyrrhic victory)は、「損害が大きく、得るものが少ない勝利」、つまり「割に合わない」という意味の慣用句である。
Wikipedia
古代ギリシアのエペイロス王で、戦術の天才と謳われたピュロスの故事に由来する。
ふ
ファティマの聖母
ファティマの聖母(ファティマのせいぼ、葡: Nossa Senhora de Fátima)は、ポルトガルの小さな町ファティマで起きた、カトリック教会が公認している、聖母の出現の一つ。ローマ教皇庁は奇跡として公に認めたが、第三の予言は長年にわたり秘匿した。何万もの群衆を前に太陽が狂ったように回転して見えたり、水源のないところから水が湧き、飲む者に奇跡的な治癒があったりしたことから、1930年10月13日現地管区レイリア司教によってこの出現は公認され、同年教皇ピオ12世は同地に巡礼する者への贖宥(免償)を宣言した。1967年には教皇庁により最初の聖母の出現のあった5月13日がファティマの記念日に制定され、歴代ローマ教皇が巡礼に訪れたり、この出現のメッセージに基づき世界の奉献を行った。
Wikipedia
ブアメードの血
ファヨールの渡り板
ファラリスの雄牛
ファラリスの雄牛(ファラリスのおうし)とは、古代ギリシアで設計されたという、処刑のための装置である。
Wikipedia
シチリア島アグリジェントの僭主であったファラリス(英語版)は、目新しい死刑方法をとりいれたいと思っていた。アテナイの真鍮鋳物師であったペリロスが、それにこたえてこの装置を考案し、ファラリスに献上した。
フィンブルの冬
フィンブルの冬(フィンブルのふゆ。古ノルド語: Fimbulvetr、英語: Fimbulwinter)は、北欧神話における世界の終わりである「ラグナロク」 が差し迫った、その前兆となる出来事である。フィンブルヴェト、フィムブルヴェトとも。
Wikipedia
フーコーの振り子
フーコーの振り子(フーコーのふりこ、フランス語:Pendule de Foucault)は、長い振り子(通常10m以上)の底に質量の大きいおもりをつけたもので、地球が自転していることの証明に使用される。レオン・フーコーが1851年1月8日にパリのパンテオンで公開実験を行い、地球の自転を証明した。
Wikipedia
フェルマーの最終定理
フェルマーの最終定理(フェルマーのさいしゅうていり、Fermat’s Last Theorem)とは、3 以上の自然数 n について、xn + yn = zn となる自然数の組 (x, y, z) は存在しない、という定理のことである。フェルマーの大定理とも呼ばれる。フェルマーが驚くべき証明を得たと書き残したと伝えられ、長らく証明も反証もなされなかったことからフェルマー予想とも称されたが、フェルマーの死後360年経った1995年にアンドリュー・ワイルズによって完全に証明され、ワイルズの定理あるいはフェルマー・ワイルズの定理とも呼ばれるようになった。
Wikipedia

ブッダの歯
フランクリンの凧
フラットウッズの怪物
フラットウッズ・モンスター(Flatwoods Monster)は、1952年9月12日にアメリカ合衆国ウェストヴァージニア州のブラクストン郡フラットウッズの町でUFOとともに目撃されたといわれる有名な「宇宙人」、あるいは未確認生物である。
Wikipedia

フリャジノの証人
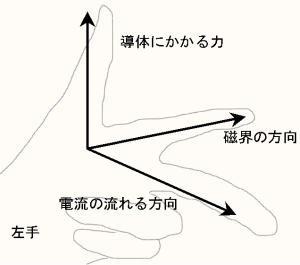
フレミングの法則
フレミング左手の法則(フレミングひだりてのほうそく、英: Fleming’s left hand rule)または、フレミングの左手の法則は、ジョン・フレミングによって考案された、磁場内において電流が流れる導体に力が発生する現象(ローレンツ力)の、それぞれの向きの関係を示す方法である。
Wikipedia
プロクルステスの寝台
ブロッケンの妖怪
ブロッケン現象(ブロッケンげんしょう、英: Brocken spectre)とは、太陽などの光が背後からさしこみ、影の側にある雲粒や霧粒によって光が散乱され、見る人の影の周りに、虹と似た光の輪となって現れる大気光学現象。
Wikipedia

プロビデンスの目
プロビデンスの目(プロビデンスのめ、英: Eye of Providence)とは、目が描かれたキリスト教における意匠。プロビデンスはキリスト教の摂理という意味で、神の全能の目(英: all-seeing eye of God)を意味する。光背や、三位一体の象徴である三角形としばしば組み合わせて用いられる。
Wikipedia
プロメテウスの火
プロメーテウス(古代ギリシャ語: Προμηθεύς、Promētheús [ pro.mɛː.tʰeú̯s])は、ギリシア神話に登場する男神で、ティーターンの一柱である。イーアペトスの子で、アトラース、メノイティオス、エピメーテウスと兄弟、デウカリオーンの父。ゼウスの反対を押し切り、天界の火を盗んで人類に与えた存在として知られる。また人間を創造したとも言われる。日本語では長音を省略してプロメテウスと表記されることもある。ヘルメースと並んでギリシア神話におけるトリックスター的存在であり、文化英雄としての面を有する。
Wikipedia
フロラの滝
へ
ベイトソンの鐘楼
ベイリーの数珠
ベイリー・ビーズ(Baily’s beads)とは、日食の際に月が太陽を隠し、月表面の凹凸の地形によって日光がビーズのように見える現象である。ベイリーズ・ビーズ、ベイリーの数珠ともいう。1836年にこの現象について初めて正しい説明を与えたフランシス・ベイリーにちなんで名付けられた。
Wikipedia

ヘスダーレンの怪光
ベツレヘムの星
ベツレヘムの星(ベツレヘムのほし)またはクリスマスの星(クリスマスのほし)[は、東方の三博士(別名「東方の三賢者」「東方の三賢王」)にイエス・キリストの誕生を知らせ、ベツレヘムに導いた、キリスト教徒にとって宗教的な星である。マタイによる福音書によれば、博士たちは星の出現に霊感を受けて「東方」からエルサレムまで旅をした。
Wikipedia
ベツレヘムの星は八芒星(オクタグラム)で表現される。
ヘラクレスの塔
ヘラクレスの塔(ヘラクレスのとう、ガリシア語・スペイン語共にTorre de Hércules)またはエルクレスの塔(エルクレスのとう)は、スペイン・ガリシア州のア・コルーニャ県の県都ア・コルーニャの中心部から2.4キロメートル離れた半島に建つローマ建築の灯台である。海抜57メートルの丘に建つこの塔は55メートルの高さがあり、スペインにおいてチピオーナ灯台(スペイン語版) (62m) についで高い灯台である。灯台からは北大西洋を一望することができる。20世紀まではブリガンティウムの塔 (Farum Brigantium) の名で知られていた。
Wikipedia
1791年に改築工事が施されたものの、ローマ時代に建築されてから既に約1,900年が経過しているにも関わらず、ヘラクレスの塔は21世紀になった今もなお現役の灯台として利用されている。2009年6月27日、UNESCOの世界遺産に登録された。

ベルメスの顔
ベルメスの顔(ベルメスのかお、Caras de Bélmez)は、スペインアンダルシーア州ハエン県のベルメス・デ・ラ・モラレーダの民家で発生した現象。その家のコンクリート床に、顔のような染みが浮かび上がるというものである。
Wikipedia

ペレーの毛
ペレーの毛(ペレーのけ、Pele’s hair)とは、火山の爆発の際に、マグマの一部が吹き飛ばされ空中で急速冷却し髪の毛のようになったもののことを言う。非常に軽いため数km先まで風で運ばれる。ペレーの涙と同じように、火山噴出物の一つである。火山毛(かざんもう)ともいう。ペレーはハワイに伝わる火山の女神のことである。
Wikipedia
おもに玄武岩質の火山ガラスからなる褐色の細い単繊維であり、典型的なものは断面が円形に近く、直径は0.5mmより細い。長さは最大2mにおよぶことがある。キラウエアに限らずニカラグアのマサヤ火山等でも知られる。
ペレーの涙
ペレーの涙(ペレーのなみだ、Pele’s tear)とは、火山の爆発の際にマグマの小さなかたまりが固結したガラス質の粒のことである。火山噴出物の一つ。火山涙(かざんるい)ともいう。
Wikipedia
流動性の高いマグマが爆発的に噴火したのち、急冷固結することで形成される。大きさは数mmから1cm程度のものが一般的である。
玄武岩質のマグマから産するため、ハワイでよく見られる。名前の由来である「ペレー」もハワイの女神の名である。日本では長崎県五島市の鬼岳などごく一部の火山でのみ産する。

ヘレナの釘
聖釘(せいてい)は、聖遺物のひとつで、イエス・キリストが磔にされた際に手足に打ちつけられた釘であるとキリスト教内で言い伝えられているもの。
Wikipedia
ヘテロストラトスの名誉
ヘロンの蒸気機関
ヘンペルの鴉
ヘンペルのカラス (Hempel’s ravens) とは、ドイツのカール・ヘンペルが1940年代に提出した、帰納法が抱える根本的な問題(「帰納法の問題(英語版)」)を喚起する問題である。「カラスのパラドックス」とも呼ばれるが、パラドックスとして扱うべきかどうかには異論もある。
Wikipedia
ベンハムの独楽
ベンハムの独楽 (ベンハムのこま)とは、イギリスのおもちゃ製造業者であるチャールス・ベンハム(en:Charles Benham)の名に由来する独楽(こま)である。主観色(錯視)の実験として有名。ベンハムは、1895年に図に示したように上面を塗り分けた独楽を発売した。
Wikipedia

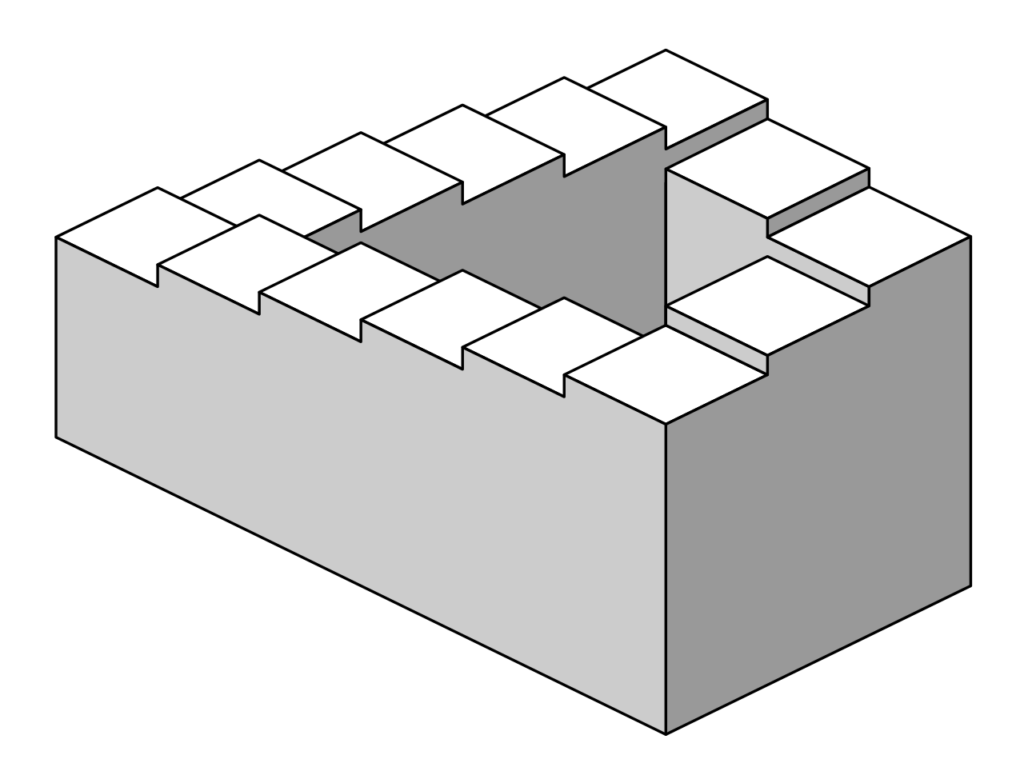
ペンローズの階段
ペンローズの階段(ペンローズのかいだん、Penrose stairs)は、ライオネル・ペンローズと息子のロジャー・ペンローズが考案した不可能図形である。
Wikipedia
ほ
ポルピュリオスの樹
ま行
ま
マーフィーの法則
マーフィーの法則(マーフィーのほうそく、英: Murphy’s law)とは、「失敗する余地があるなら、失敗する」「落としたトーストがバターを塗った面を下にして着地する確率は、カーペットの値段に比例する」をはじめとする、先達の経験から生じた数々のユーモラスでしかも哀愁に富む経験則をまとめたものである(それが事実かどうかは別)。多くはユーモアの類で笑えるものであるが、精神科医や学者の中には、認知バイアスのサンプルとして捉えることが可能なものも少数あるとの見方もある。歌手の嘉門達夫は、CDシングル『マーフィーの法則』を発表している。ビジネス本、自己啓発本として出版もされた。
Wikipedia

マクスウェルの悪魔
マクスウェルの悪魔(マクスウェルのあくま、Maxwell’s demon)とは、1867年ごろ、スコットランドの物理学者ジェームズ・クラーク・マクスウェルが提唱した思考実験、ないしその実験で想定される架空の、働く存在である。マクスウェルの魔、マクスウェルの魔物、マクスウェルのデーモンなどともいう。 分子の動きを観察できる架空の悪魔を想定することによって、熱力学第二法則で禁じられたエントロピーの減少が可能であるとした。 熱力学の根幹に突き付けられたこの難問は1980年代に入ってようやく一応の解決を見た。
Wikipedia
マクデブルグの半球
マクデブルクの半球(マクデブルクのはんきゅう、ドイツ語:Magdeburger Halbkugeln)は、17世紀のドイツでオットー・フォン・ゲーリケが行なった、大気圧を示す実験である。
Wikipedia
半球は、内側がくぼんだ2つの金属製の半球だった。縦に2つに割ったメロンをイメージすると分かりやすい。この2つの半球はすきまなく接合するように作られた。この2つを合わせ、ゲーリケ自らが発明した真空ポンプで中の空気を抜いた。間には濡らした動物の皮をパッキンとして使用した。こうすると半球はぴったりくっつき、どんなに引っ張っても外れなかった。これは、半球の外側の大気圧によるものである。
マナの壺
マラカナンの悲劇
マラカナンの悲劇またはマラカナッソ(西: Maracanazo, 葡: Maracanaço)は、1950年7月16日にブラジル・リオデジャネイロのエスタジオ・ド・マラカナンで行われたFIFAワールドカップ・ブラジル大会(1回目)の決勝リーグ第3戦(優勝が決まる試合ではあったが、1950年の大会は決勝トーナメント方式を採用していなかったため「決勝戦」ではない。)、ブラジル対ウルグアイの試合でブラジルが優勝を逃したことを指す通称である。
Wikipedia

マラディの角度
マラルディの角度はその形になって最も安定する自然の摂理の角度なのである。 9 直角+19.5度の109.5度と、その補角である直角-19.5度の70.5度は、正4面体の中心角と2面角として現れているが、3次元の中で3軸直交している正6面体の中にも、この重要な2つの角度が潜んでいる。
zone2
み
ミネルヴァの泉
ミネルウァ(ラテン語: Minerva)は、詩・医学・知恵・商業・製織・工芸・魔術を司るローマ神話の女神。英語読みはミナーヴァ。俗ラテン語などに基づくミネルヴァという読みでも知られる。
Wikipedia
芸術作品などでは、彼女の聖なる動物であり知恵の象徴でもあるフクロウと共に描かれることが多い。音楽の発明者でもある。ギリシア神話のアテーナーと同一視される。
ミノタウロスの迷宮
ミーノータウロス(古希: Μινώταυρος, Mīnōtauros, ラテン語: Minotaurus, 英語: Minotaur)は、ギリシア神話に登場する牛頭人身の怪物である。クレータ島のミーノース王の妻パーシパエーの子。長母音を省略してミノタウロスとも表記される。
Wikipedia
ミューゼスの海
む
め
メアリーの部屋
メアリーの部屋(メアリーのへや、Mary’s Room)またはスーパー科学者メアリー(スーパーかがくしゃメアリー、Mary the super-scientist)とは、フランク・ジャクソンが「随伴現象的クオリア」”Epiphenomenal Qualia” (1982)、さらに「メアリーが知らなかったこと」”What Mary Didn’t Know” (1986) という論文の中で提示した、哲学的思考実験である。この思考実験は、性質二元論または中立一元論の立場から物理主義(心的なものも含む宇宙は全て物理的なものであるという立場)に対して展開されるもので、しばしば知識論法(Knowledge Argument)とも呼ばれる。最近、この思考実験が発表された後に出来した議論がまとめられ、『メアリーに首ったけ』”There’s Something About Mary” (2004) として公刊された。これには、ダニエル・デネット、デイヴィド・ルイス、ポール・チャーチランドなどの回答も採録されている。
Wikipedia

メデューサの頭
メデューサの頭(メデューサのあたま、英: Caput medusae)は、パームツリーサインとも呼ばれる腹部の血管徴候である。
Wikipedia
メビウスの輪
メビウスの輪(モェビウスのわ、[ˈmøːbi̯ʊs]のわ、Möbius loop)は、帯状の長方形の片方の端を180°ひねり、他方の端に貼り合わせた形状の図形(曲面)である。メービウスの帯ともいう。
Wikipedia
数学的には向き付け不可能性という特徴を持ち、その形状が化学や工学などに応用されているほか、芸術や文学において題材として取り上げられることもある。

メルケルの斜方形
メルケルの斜方形(ドイツ語: Merkel-Raute)またはメルケルのひし形は胸の下に指が触れあうように手を置くハンドジェスチャーで、「斜方形」(Raute)は親指と人差し指が四角に似た形をつくることから来ている。ドイツの首相であるアンゲラ・メルケルの代名詞的な仕草であり、「おそらく世界でも有数の誰もが見覚えあるハンドジェスチャーである」。
Wikipedia
も
モーセの十戒
モーセの十戒(十誡、じっかい、ヘブライ語: עשרת הדיברות、英: Ten Commandments)とは、モーセがユダヤ民族を代表して神から与えられた10の戒律のこと。
Wikipedia
モンテスマの復讐
や行
や
ヤコブの梯子
ヤコブの梯子 (旧約聖書) – 旧約聖書の創世記28章10–12節でヤコブが夢に見た、天使が上り下りしている、天から地まで至る梯子、あるいは階段。
Wikipedia

ヤンソンの誘惑
ヤンソンの誘惑(ヤンソンのゆうわく、瑞: Janssons frestelse, 英: Jansson’s temptation)は、スウェーデンの伝統的家庭料理。ヤンソン氏の誘惑(ヤンソンしのゆうわく)またはヤンソンさんの誘惑(ヤンソンさんのゆうわく)とも呼ばれている。
Wikipedia

ゆ
よ
ヨハネの黙示録
『ヨハネの黙示録』(ヨハネのもくしろく 古代ギリシア語: Ἀποκάλυψις Ἰωάννου、ラテン語: Apocalypsis Iōannis、英語: Revelation)は、『新約聖書(クリスチャン・ギリシャ語聖書)』の最後に配された聖典であり、『新約聖書』の中で唯一預言書的性格を持つ書である。
Wikipedia
ら行
ら
ライナスの毛布
ライヘンバッハの滝
ライヘンバッハの滝(ライヘンバッハのたき、独: Reichenbachfall)は、スイスにある落差250メートル(656フィート)、幅90メートル(300フィート)の滝である。アルプス山脈でも最も高所にある滝のひとつである。
Wikipedia
ライラックの瞳
ラファエロの間
ラファエロの間(伊:Stanze di Raffaello)は、バチカン宮殿にある4つの部屋の総称である。この4つの部屋で一続きの応接室を構成しており、教皇庁の一部として公開されている。ラファエロ・サンティと彼の弟子らの手による多くの著名なフレスコ画が展示されている。ミケランジェロによるシスティナ礼拝堂の天井画とともに、フレスコ画としては盛期ルネサンスを代表する作品として広く知られている。
Wikipedia
ラプラスの悪魔
ラプラスの悪魔(ラプラスのあくま、英:Laplace’s demon)とは、主に近世・近代の物理学分野で、因果律に基づいて未来の決定性を論じる時に仮想された超越的存在の概念。「ある時点において作用している全ての力学的・物理的な状態を完全に把握・解析する能力を持つがゆえに、宇宙の全運動(未来を含む)までも確定的に知りえる」という超人間的知性のこと。フランスの数学者、ピエール=シモン・ラプラスによって提唱された。ラプラスの魔物あるいはラプラスの魔とも呼ばれる。
Wikipedia
ラングトンの蟻
ラングトンのアリ(英: Langton’s ant)は、クリストファー・ラングトンが発明した単純な規則で記述される2次元チューリングマシンである。
Wikipedia
り
リービッヒの最小律
リービッヒの最小律(リービッヒのさいしょうりつ)は、植物の生長速度や収量は、必要とされる栄養素のうち、与えられた量のもっとも少ないものにのみ影響されるとする説。ドイツの化学者・ユーストゥス・フォン・リービッヒが提唱した。
Wikipedia
リービッヒは、植物は窒素・リン酸・カリウムの3要素が必須であるとし、生長の度合いは3要素の中でもっともあたえられる量の少ない養分によってのみ影響され、その他2要素がいくら多くても生長への影響はないと主張した。後に養分以外の水・日光・大気などの条件が追加された。
現在では、それぞれの要素・要因が互いに補い合う場合があり、最小律は必ずしも定まるものではない、とされている。

リチャードソンの夢
る
ルドルフの数
ルドルフ数……円周率(えんしゅうりつ)は、円の周長の、直径に対する比率として定義される数学定数である。通常、ギリシア文字 πで表される。数学をはじめ、物理学、工学といった様々な科学分野に出現し、最も重要な数学定数とも言われる。
Wikipedia
円周率は無理数であり、その小数展開は循環しない。円周率は、無理数であるのみならず、超越数でもある。
ルビンの壺
ルビンの壺(ルビンのつぼ、Rubin’s vase)とは、1915年頃にデンマークの心理学者エドガー・ルビンが考案した多義図形。ルビンの顔(ルビンのかお、Rubin face)、図地の壺(ずちのつぼ、figure-ground vase)、ルビンの盃・ルビンの杯(ルビンのさかずき、Rubin’s goblet-profile)とも。
Wikipedia

ルルドの泉
れ
レボンボの骨
レボンボの骨(レボンボのほね)は、南アフリカとスワジランドの間にあるレボンボ山脈で発見された、刻み目のついたヒヒの腓骨で作られた骨角器。刻み目の部分が変わっていることは、異なる刃先を使ったことを示しており、この骨の発見者である Peter Beaumont は、このことが世界中で発見される刻み目と同じように、儀式に参加している間にできた刻みだという証拠であると考えている。
Wikipedia
ろ
ロートスの木
ロートスの木(Lotus tree、ギリシア語:λωτός)は、ギリシア神話の2つの話に登場する植物である。ホメーロスの『オデュッセイア』では、心地良い眠りに誘う実をつける木で、ロートパゴス族と呼ばれる島民の唯一の食物として描かれている。彼らがロートスの実を食べると、彼らは友人や家のことも忘れ、故郷の土地に戻って安逸な生活を送るという願望も失ってしまったという。この植物の候補としては、アジア原産の落葉樹で、約25フィートの高さまで成長し黄緑色の花を咲かせるマメガキや北アフリカとガベス湾の島が原産で、ナツメに似た実をつけるZiziphus lotusであるとも言われている。
Wikipedia
ロガエスの書
ロガエスの書(ロガエスのしょ、Liber Loagaeth)は、16世紀末にエノク語で書かれた未解読の文書。ジョン・ディー博士著。別名、「エノク書」と呼ばれるが、旧約聖書の偽典の一つである『エノク書』とは別物。
Wikipedia
本書はエリザベス朝の学者ジョン・ディーが行った天使との交霊実験の産物とされるエノク語文献のひとつである。霊視者としてジョン・ディーの助手を務めたエドワード・ケリーによって書きとめられた。49×49の升目の多数の文字表で構成されている。大英図書館スローン文庫の手稿3189番がこれに当たる。
ロッシュの限界
ロッシュの限界 (ロッシュげんかい、英語:Roche limit)とは、惑星や衛星が破壊されずにその主星に近づける限界の距離のこと。その内側では主星の潮汐力によって惑星や衛星は破壊されてしまう。
Wikipedia
ロレットチャペルの螺旋階段
ロングヌスの槍
ロンバルディアの鉄王冠
ロンバルディアの鉄王冠(ロンバルディアのてつおうかん、イタリア語: Corona FerreaまたはCorona di Ferro、英語: Iron Crown of Lombardy)は、中世前期につくられたヨーロッパで最も古い王冠の一つであるとともに、キリスト教の聖遺物である。ラテン語に由来するコローナ・フェッレア(Corona Ferrea)の名でも呼ばれる。
Wikipedia
この王冠はイタリア・ロンバルディア州の州都ミラノにほど近いモンツァの大聖堂 (Duomo of Monza)
において保管されており、はじめランゴバルド王国(ロンバルディア王国)の、のちに中世イタリア王国の王権の象徴とされた。

わ行
わ
ワインの涙
ワインの涙(ワインのなみだ)は、グラスワインの液面近くのガラス内壁に絶え間なく形成されては零れ落ち続ける無色の液滴。特にアルコール度数の高いワインで見られる。Wine legs(ワインの脚)やcurtains(カーテン)、church windows(教会の窓)とも呼ばれる。
Wikipedia





